[Algorithm] Union Find

#1 About Union-Find

유니온 파인드는 여러 개의 노드가 주어졌을 때 특정한 노드들이 같은 그룹에 속해있는지 판별하고 여러 개의 그룹 노드를 하나로 합치는 작업을 수행할 때 사용되는 알고리즘이다.

이름에서 유추 가능하듯 노드를 한 그룹으로 합치는 "유니온(Union)"연산과 노드가 특정 그룹 내에 존재하는지 판별하는 "파인드(Find)"연산으로 이루어진다.

 

Union-Find 알고리즘을 직접 구현해 보자.

우선 크기가 5인 배열을 모두 -1로 초기화해준다. 

각 배열의 원소값은 해당 인덱스의 부모 노드를 가리킨다. 

배열의 원소가 -1이라면 부모 노드가 자기 자신 즉, 루트노드라는 의미이다.

 

union(1, 5)

노드1과 노드5를 유니온 연산을 진행한다. 

노드5는 노드1의 자식노드가 되며 배열의 5번째 인덱스를 인덱스 5의 부모인 1로 업데이트한다.

이제 1과 5는 같은 그룹이다.

 

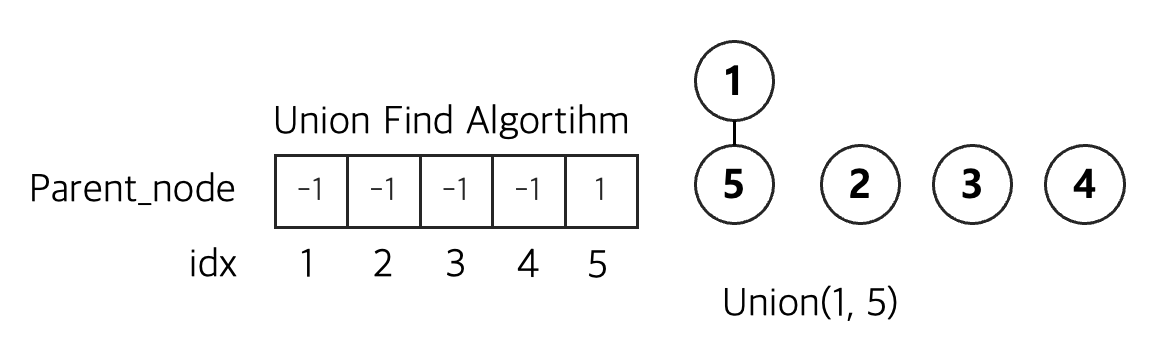
union(1,2)

노드1과 노드2를 유니온 연산을 진행한다. 

마찬가지로 노드2를 노드1의 자식으로 포함시키며, 배열의 2번째 인덱스 값을 1로 업데이트한다.

 

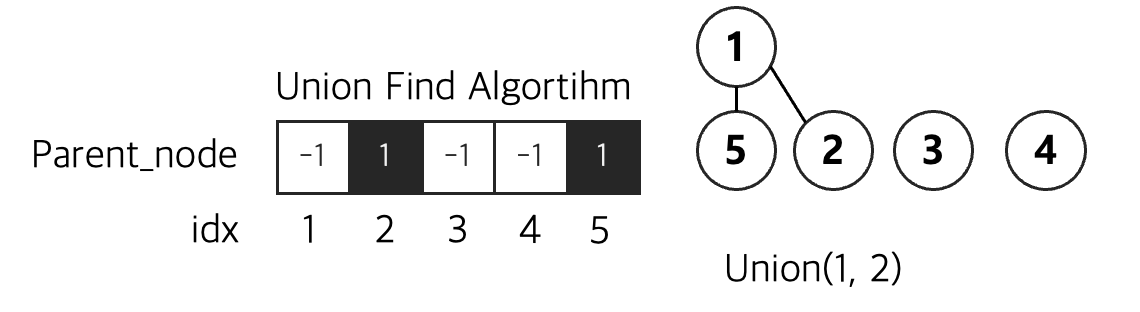
union(3,4) union(1,4)

다음으로 union(3,4), union(1,4) 연산을 차례로 진행한 예제를 살펴보자.

union(3,4) 연산까지는 지금까지 한대로 하면 되는데, union(1,4)에서 두 가지 케이스가 발생한다. 

이때 노드4를 노드1의 자식으로 두면 안되고, 노드3을 노드1의 자식으로 세팅해야 한다. 

 

최종적으로 배열과 그래프는 아래와 같은 상태가 된다. 

find 연산은 간단하다.

노드4의 그룹을 확인하고 싶다면 부모노드를 차례로 타고 올라가서 값이 -1인 노드 (루트노드)의 인덱스가 노드4가 속한 그룹 번호이다.

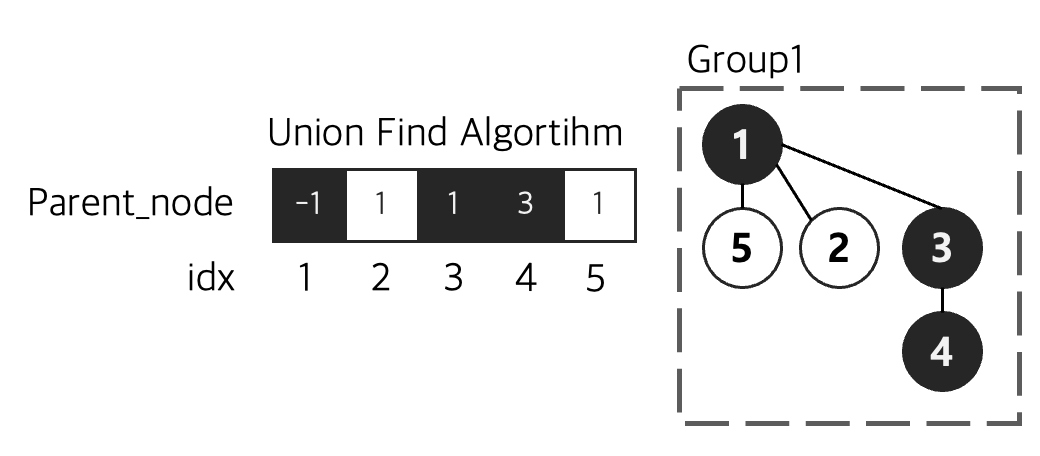
find 함수는 인자로 노드 x (해당 노드가 몇 번 그룹에 속하는지 탐색할 노드) 를 받는다.

만약 인자로 받은 노드를 인덱스로 하는 배열 안의 값이 음수 (-1) 이라면 루트노드라는 뜻이기에 해당 노드를 반환한다.

만약 노드의 값이 -1이 아니면 노드가 루트 노드가 아니며, 부모 노드가 존재한다는 뜻이기에 재귀 호출로 부모 탐색을 진행한다.

vector<int> p(5, -1);

// find 연산 
int find (int x) {
    if (p[x] < 0) return x; // 정점 도달
    return find(p[x]); // 부모 탐색 
}

 

uni 함수는 인자로 합칠 2개의 노드(u, v)를 받는다.

앞서 구현한 find 함수를 사용해 두 노드의 루트 노드를 탐색한다.

만약 루트 노드가 동일하다면 같은 그룹에 속한다는 의미이며, 루트 노드가 다르다면 서로 다른 그룹에 속한 노드라는 뜻이기에 v노드를 u노드의 자식으로 세팅한다.

// union 연산
// 정점 u가 속한 트리의 루트를 탐색. 
// v가 속한 트리의 루트를 찾은 후 "v가 속한 트리의 루트"를 "u가 속한 트리의 자식"으로 설정 
bool uni(int u, int v) {
    u = find(u); // 정점 u가 속한 트리의 루트를 탐색 
    v = find(v); // 정점 v가 속한 트리의 루트를 탐색 
    if (u == v) return false; // 정점 u와 정점 v가 같다면, 같은 그룹
    p[v] = u; // 정점 v가 속한 트리의 루트를 정점 u의 자식으로 설정 
    return true; 

}

 

#2 Union Find Usage 

1. Cycle Detection - 그래프 내부에서 사이클이 존재하는지 판별할 때 사용한다. 

2. Kruskal's Algorithm - 최소 신장 트리 (MST)를 만드는 알고리즘인 크루스칼 알고리즘에서 유니온 파인드 자료구조가 사용된다. 

3. Network Connectivity - 노드와 연결선이 주어졌을때 두 노드가 서로 연결되어 있는지 판별할 때 사용된다.

 

Cycle Detection

유니온 파인드의 첫 번째 사례인 Cycle Detection 에서 단순히 그래프 내부의 사이클 존재 여부만 탐색할 경우에는 DFS를 사용하는 아이디어도 가능하다. 

"그래프가 어떠한 상태에 놓여져 있는지"를 먼저 파악해 보면 어떤 알고리즘을 채택하는 것이 효율적인지 판별할 수 있다. 

 

정적 그래프에서 이미 모든 간선과 노드의 정보가 주어진 상태에서 사이클을 존재 유무를 한 번에 판별하는 상황에서는 DFS 알고리즘을 채택하는 것이 직관적이다. 

하지만 동적 그래프에서 간선이 하나씩 추가되는 상황에서 사이클 여부를 판별하는 상황에서는 Union Find 알고리즘을 떠올리는 것이 바람직하다. 

예시로 BOJ 20040 사이클게임 같은 문제와 같이 실시간으로 그래프의 상태가 변하는 상황에서 DFS를 적용해 매 번 모든 그래프의 노드를 탐색하는 것은 굉장히 비효율적이다. 

https://www.acmicpc.net/problem/20040

 

Network Connectivity 

백준 7511 소셜 네트워킹 어플리케이션 문제 또한 유니온 파인드 알고리즘의 3번째 문제 상황을 대입해 보기에 좋은 문제이다.

마찬가지로 해당 문제도 단순히 모든 상황에서 DFS/BFS를 사용해 두 친구 노드가 연결되어 있는지 탐색하고자 하면 시간초과가 발생한다. 

하지만 유니온 파인드 알고리즘을 적용하면 어렵지 않게 노드가 같은 그룹에 속하는지 판별 가능하다. 

(BFS/DFS 알고리즘을 사용하더라도 전처리 과정을 거치면 시간 내에 통과하기는 한다.)

https://www.acmicpc.net/problem/7511

 

---

code

https://github.com/novvvv/PS2025/blob/main/202509/7511.cpp

https://github.com/novvvv/PS2025/blob/main/202509/20040.cpp